|
Las anomalías, lejos de constituir simples desviaciones,
pueden ser asociadas al estatuto de lo desconocido en el inconsciente humano.
Por sus características, estas no adquieren valor explicativo
dentro del marco de las formas clásicas.
Allí donde los objetos fractales se manifiestan mediante rupturas y discontinuidades,
se configura un espacio de inscripción que contribuye a la formación del inconsciente.
La autoorganización del mundo no se limita a los dominios formales de la ciencia,
sino que se expresa en la música, el arte, los vínculos, lo sagrado;
en suma, en fenómenos que carecen de ley universal.
Lo fractal nombra precisamente esta dimensión.
De allí que la conciencia del sujeto no se presente como una totalidad armónica,
sino como un ensamblaje de elementos fragmentarios,
es decir, como una estructura atravesada por lo quebrado:
el inconsciente, que remite siempre a aquello que ha quedado fuera,
a saber, la historia.
Anticipar los fenómenos mediante los fractales implica aprender a escuchar
el sonido de las formas.
Su leitmotiv consiste en otorgar estatuto ontológico
a aquello que ha roto con la regla.
Por esta razón, lo que no puede ser enunciado a través de las figuras clásicas
encuentra en lo fractal un modo de decirse.
Los fractales no operan como meras representaciones,
sino como dispositivos de disciplina epistemológica,
preparando a la inteligencia para comprender las condiciones de acceso a la realidad.
|
Lo fractal no es un resultado directo de las matemáticas del siglo XX,
sino una rama que nació del legado de investigadores heterodoxos,
como Weierstrass (descubridor de la primera función continua y no diferenciable),
Cantor, Peano, Lebesgue o Hausdorff, a los que siguieron después de 1925
Besicovitch, Bolzano y Cesàro.
Estos matemáticos no se han destacado por el estudio empírico de la naturaleza,
pero sus creaciones esconden un mundo de interés para aquellos que
perciben la complejidad de la naturaleza tratando de imitarla.
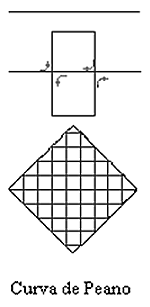
G. Cantor y Peano fueron los primeros en desarrollar estos objetos fractales
para dimensionar el mundo, apartándose de los postulados de Euclides y de la
geometría analítica de Descartes. El matemático Cantor sostiene que un espacio de dimensión uno
tiene la misma cantidad de puntos que uno de dimensión tres. La formulación de Cantor
solamente dice: ¿qué le sucede a un hilo luego de ovillarlo?: algo raro, pasa de 1 dimensión pasó a 3.
Según este ejemplo, la hipótesis de Cantor sustenta la existencia de un nuevo suelo para ver el mundo y lo que está contenido en él. En este suelo descansa el binomio orden-caos que vemos en el campo de la meteorología, la economía política, los átomos. El binomio orden-caos es estructurado (armonizado) por el “infinito en acto”, que es donde se autoorganiza lo fractal en aproximación con el mundo. A partir de aquí, lo infinito ocupará el lugar que tenían las causas para Aristóteles. En efecto, el mundo y lo que hay en él: sus leyes, no son fijas, inmóviles, totales, sino que se disuelven, se deslizan, se fragmentan, pues los procesos naturales son emergentes, es decir, evolucionan, se autoorganizan, "la naturaleza no da saltos" 1 escribió G. W. Leibniz, en el siglo XVII, en Alemania.
De allí se sigue la pertinencia epistemológica de la geometría fractal como dispositivo conceptual capaz de operar una ruptura con los esquemas clásicos de inteligibilidad. La hipótesis del infinito en acto no debe entenderse como una extensión cuantitativa del espacio euclidiano, sino como una reorganización cualitativa de las condiciones mismas bajo las cuales un fenómeno deviene pensable.
|

|

En términos bachelardianos, la geometría fractal constituye un claro ejemplo de obstáculo epistemológico superado: desarticula la intuición geométrica inmediata heredada del sentido común y de la física clásica, imponiendo una reconstrucción racional del objeto. No se trata de describir una realidad previamente dada, sino de producir un nuevo objeto teórico, irreductible a las categorías de continuidad, regularidad y homogeneidad propias de la matemática clásica.
Los objetos fractales, particularmente aquellos generados mediante procedimientos informáticos, permiten modelizar procesos caracterizados por la multiplicidad dimensional, la irregularidad estructural y la autoorganización. Tales modelos no representan fenómenos simples, sino que operan como esquemas de inteligibilidad de dinámicas complejas, en las cuales el orden emerge de la inestabilidad y la fluctuación. En este sentido, la geometría fractal no describe estados, sino procesos.
Desde una perspectiva próxima a la epistemología histórica de Canguilhem, estas estructuras no deben evaluarse en función de su adecuación a una norma previa, sino como productoras de nuevas normas de racionalidad. Lo que en el marco euclidiano aparecía como anomalía o patología geométrica, se redefine aquí como forma legítima de organización. La anomalía deja de ser un defecto para devenir principio constitutivo del objeto.
Esta transformación conceptual inscribe a la geometría fractal en una ruptura histórica con el paradigma newtoniano, basado en la reversibilidad, la linealidad y la estabilidad de las leyes. Frente a dicho paradigma, la matemática contemporánea incorpora la irreversibilidad, la discontinuidad y la emergencia como rasgos estructurales de los fenómenos. No se trata de excepciones locales, sino de propiedades fundamentales de los sistemas complejos.
En consonancia con los desarrollos de Prigogine, los fractales permiten pensar la autoorganización como resultado de procesos alejados del equilibrio, donde el azar y la inestabilidad no constituyen residuos explicativos, sino condiciones productivas. El orden ya no es anterior al proceso, sino que emerge de él, de manera contingente e históricamente situada.
Desde este marco, la interrogación sobre la dimensión del espacio deja de ser una cuestión meramente formal para convertirse en un problema epistemológico central. La posibilidad de pensar espacios de dimensión no entera o variable implica una revisión profunda de las categorías mediante las cuales se estructura la experiencia científica del mundo.
Finalmente, el valor epistemológico de los patrones fractales reside en su capacidad para ampliar el campo de lo pensable, mostrando que la racionalidad científica no se reduce a la búsqueda de formas simples, sino que puede incorporar la complejidad, la irregularidad y la inestabilidad como principios positivos de conocimiento.
En este sentido, la geometría fractal se inscribe plenamente en el horizonte del pensamiento complejo, no como una mera técnica matemática, sino como una transformación profunda de las condiciones históricas de producción del saber científico.
Río de la Plata, 30 de noviembre de 2025
1 — Gottfried Wilhelm Leibniz, Nuevos Ensayos Acerca del Entendimiento Humano, §59. Volver al texto
|
|




















