Los elementos de nuestra realidad cotidiana, al igual que todos nuestros antepasados —todo nuestro pasado sin conocer—, y también, todos nuestros descendientes —todo nuestro futuro—, existen y están ahí como diferentes e individuales trayectorias de interacciones que se entrecruzan entre las partículas elementales del cosmos...

El significante fractal (del latín medieval: fractus, evoca lo interrumpido, roto o irregular) es acuñado por el Ingeniero Aeronáutico Benoit Mandelbrot † 2010, que trabajaba como investigador en IBM. 1

Consideremos esta hipótesis: la conciencia junto al invento de la verdad son herramientas útiles, que a modo de prótesis, nos sostienen en el mundo. Son producciones de la metafísica, que nuestro sistema nervioso adoptó, porque ambas se constituyen como metáforas que se han olvidado que lo son. Es decir, el cerebro desconoce que son ilusiones, condensaciones, configuraciones de imágenes, metonimias, convenciones del lenguaje, consensos, acuerdos y desacuerdo que se cristalizaron por el habla desde la infancia como dado, esto es, como realidad.


Cuando miramos alrededor nuestro, el mundo, creemos en eso que sentimos, es decir, tenemos confianza en los datos de nuestra percepción, esto es, la vista, el oído, el tacto, el olor. Por ejemplo, al ver mí dedo, creo está ahí, y puedo afirmar también que ese es efectivamente mí dedo.

Pero si hay que dar una descripción de cómo es mí dedo, voy tender a decir que es como una ramita, un palito, voy a tratar de explicar cómo es mí dedo con esquemas geométricos. De hecho, vivimos en un entorno geométrico, en donde nos movemos, y además, le agregamos un tiempo, cuya forma de representación es siempre lineal y constante.

De lo anterior resulta que la creencia que tenemos de las cosas, es decir, de lo que vemos en un punto espacio temporal, se llevan a cabo por ciertos modelos mentales para mirar, de lo contrario, no podríamos ubicarnos y ser en el mundo. Los modelos mentales son como ideas que utilizamos para acercarnos a las cosas. Ideas que nos permiten adquirir cierto dominio, por ejemplo, cuidar mí cuerpo, hablar de mis dedos y pensar los dedos de otros.

Ahora bien, si nos metemos en el mundo atómico, notaremos que la simplicidad siempre resultó más atractiva que la complejidad. Veamos el caso de un cuerpo rodeado por otros como si estuvieran bailando alrededor de él, ¿qué es lo primero que nos viene al pensamiento?, es decir, ¿con qué asociamos?: seguro que con la idea de átomo. A simple vista, nuestra hipótesis atómica (la existencia de un centro –un núcleo compuesto por protones y neutrones– a cuyo alrededor giraban los electrones) es la misma que postula la astronomía de Nicolás Copérnico, como la idea de un sistema planetario cuyo centro es el sol o una galaxia.

Asimismo, cuando observamos un cuerpo rodeado por otros como si estuvieran bailando alrededor de él nos hace creer, ver y decir que la estructura interna de la materia tiene una semejanza con la estructura del macrocosmos, es decir, el sistema solar. El núcleo atómico, según esta concepción de escuela, desempeñada por el rol del Sol y los electrones, no son otra cosa sino que los planetas de ese sistema microcósmico que tenemos idealmente en la mano.

La idea de atrapar el mundo de un solo apretón responde a esquemas de pensamiento adolescentes donde la mente asiente, es decir, admite como cierta o conveniente, que todo esos elementos tienen una estructura semejante al todo, y por ende, el sujeto cree ver todo (panóptico), de modo que vincular y confundir las cosas de manera simplista se convierte inconscientente en una tarea antropomórfica y embaucadora, que se va transmitir en forma de símbolo en los miembros de la misma especie.

Ahora bien, en la primera mitad del siglo XX, el mito de los tiempos modernos de estar en presencia de la “clave del todo” empieza a esfumarse casi como una brisa. Luego de la “teoría de los cuantos” del físico danés Niels Bohr (1885-1968) se comprueba que el funcionamiento de los elementos del micro y microsistema no es el mismo y que, como fácilmente se puede apreciar: «las nubes no son esferas, las montañas no son conos, las costas no son círculos, como la corteza de un árbol no es plana ni un rayo viaja en línea recta... La naturaleza no solamente exhibe un grado mayor sino también un nivel diferente de complejidad». En efecto, la idea de tener un modelo del mundo resurge en 1975, cuando el matemático polaco de nacimiento y francés de educación Benoît Mandelbrot presenta al mundo académico de las ciencias: los “objetos fractales”.

Mandelbrot sostiene que cualquier objeto que observamos es una “parte” que se vuelve a repetir en la misma estructura general por la intrincada y persistente recursividad de los fractales (sus partes debidamente ampliadas se parecen al todo). La recursividad es un procedimiento técnico que consiste en aplicar una fórmula un número indefinido de veces al resultado mismo de una anterior aplicación esa misma fórmula. Según esto, tenemos ya una aproximación a la idea de “autosemejanza” propiedad que caracteriza la forma fractal.

La geometría fractal está compuesta por una matemática de modelos repetitivos presentes en muchas facetas de la naturaleza. Objetos como un copo de nieve, como la figura siguiente:

Como podemos ver, estudiando estas entidades matemáticas, cuyas propiedades fundamentales son la autosemejanza y la autorreferencia, se llega a representar figuras complejas, tales como árboles, hojas, formaciones rocosas, nubes o incluso rostros humanos. Todo ello partiendo de cantidades ridículas de información capaz de describirlas; algo tan sencillo como una simple fórmula matemática.

Pero..., ¿qué son los fractales?

Los fractales fueron concebidos aproximadamente en 1880 por el francés Henri Poincaré. Sin embargo, sus ideas han sido extendidas mucho más tarde fundamentalmente por los matemáticos también franceses, Gastón Julia y Pierre Fatou, hacia 1918. Se ha trabajado mucho en este campo para simular lo infinito en matemática durante varios años, pero este estudio queda congelado por los años 20. No obstante, las ideas se vuelven a renovar a partir de 1974 en IBM y es fuertemente impulsado por el desarrollo del ordenador digital.

El Profesor Mandelbrot de la Universidad de Yale por sus experimentos en ordenadores es considerado padre de la geometría fractal. Existe en su honor el fractal llamado en su propio nombre, Conjunto Mandelbrot, que ha sido descubierto por Él trabajando en el centro de investigación Thomas J. Watson. A continuación veremos el dibujo original del “conjunto Mandelbrot”:

El conjunto Mandelbrot es un nuevo universo de complejidad. Universo cuya naturaleza está compuesta por infinitas dimensiones. En nuestros días, esta forma está considerada por muchos investigadores como el objeto geométrico más complicado creado hasta el momento por el hombre. La frontera que delimita este objeto en el plano complejo es siempre algo fractal. Si bien hoy disponemos de imágenes más detalladas como las representadas al final del párrafo; cuando ampliamos alguna parte de la figura, nos topamos siempre con el mismo desconcierto: son diminutos plagios del conjunto original, es decir, minimandelbrots. No exactamente idénticos, pero sí semejantes. Conjuntamente, estos plagios de partes están llenos de filamentos cada una de las cuales vuelve a organizar un conjunto Mandelbrot cuando son ampliadas, y así ad nausean...

En la tabla inferior se puede ver otro ejemplo de la existencia de pequeñas réplicas similares al propio conjunto inicial en su interior. Para armar la secuencia se ha utilizado el programa Fractint para generar las imágenes del conjunto Mandelbrot. En efecto, partiendo del conjunto inicial se van haciendo sucesivas ampliaciones de izquierda a derecha en las tres primeras imágenes y de derecha a izquierda en las siguientes.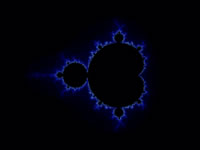

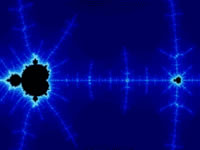
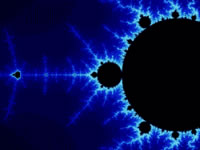
En esta sección hemos tratado de ver qué es un fractal, sobre todo, el modelo creado por el padre de los fractales. En efecto, la enorme complejidad que encierra el conjunto de Mandelbrot es válida no solo para ampliar nuestra capacidad de aprendizaje en las diversas áreas de investigación, sino también, para sentir cualitativamente el mundo natural que nos rodea.

Referencia pie de página

1- La geometría fractal de la naturaleza. Título original en inglés: The Fractal Geometry of Nature es un libro de 1982 escrito por el matemático franco-estadounidense Benoît Mandelbrot. Volver al texto